1 📑Metadata

摘要 - Recently, Transformer model, which has achieved great success in many artiﬁcial intelligence ﬁelds, has demonstrated its great potential in modeling graph-structured data. Till now, a great variety of Transformers has been proposed to adapt to the graph-structured data. However, a comprehensive literature review and systematical evaluation of these Transformer variants for graphs are still unavailable. It's imperative to sort out the existing Transformer models for graphs and systematically investigate their effectiveness on various graph tasks. In this survey, we provide a comprehensive review of various Graph Transformer models from the architectural design perspective. We ﬁrst disassemble the existing models and conclude three typical ways to incorporate the graph information into the vanilla Transformer: 1) GNNs as Auxiliary Modules, 2) Improved Positional Embedding from Graphs, and 3) Improved Attention Matrix from Graphs. Furthermore, we implement the representative components in three groups and conduct a comprehensive comparison on various kinds of famous graph data benchmarks to investigate the real performance gain of each component. Our experiments conﬁrm the beneﬁts of current graph-speciﬁc modules on Transformer and reveal their advantages on different kinds of graph tasks.

2 💡Note

2.1 论文试图解决什么问题？

To sort out the existing Transformer models for graphs and systematically investigate their effectiveness on various graph tasks.

2.2 这是否是一个新的问题？

Yes, a comprehensive literature review and systematical evaluation of these Transformer variants for graphs are still unavailable.

2.3 这篇文章要验证一个什么科学假设？

The benefits of current graph-specific modules on Transformer and reveal their advantages on different kinds of graph tasks: 1. Current models incorporating the graph information can improve the performance of Transformer on both graph-level and node-level tasks. 2. Utilizing GNN as auxiliary modules and improving attention matrix from graphs generally contributes more performance gains than encoding graphs into positional embeddings. 3. The performance gain on graph-level tasks is more significant than that on node-level tasks. 4. Different kinds of graph tasks enjoy different group of models.

2.4 有哪些相关研究？如何归类？谁是这一课题在领域内值得关注的研究员？

Limitations of GNN based on the [[message passing]] paradigm:
1. Expressive power bounded by WL isomorphism hierarchy.
2. [[over-smoothing]] problem due to repeated local aggregation.
3. [[over-squashing]] problem due to the exponential computation cost with the increase of model depth.
Three typical ways to incorporate the graph information into the vanilla Transformer:
1. GNNs as Auxiliary Modules:
  1. Build Transformer blocks on top of GNN blocks;
  2. Stack GNN blocks and Transformer blocks in each layer;
  3. Parallel GNN blocks and Transformer blocks in each layer.
2. Improved Positional Embedding from Graphs.
  1. Compress the graph structure into positional embedding vectors and add them to the input before it is fed to the vanilla Transformer model.
3. Improved Attention Matrices from Graphs.
  1. Inject graph priors into the attention computation via graph bias terms;
  2. Restrict a node only attending to local neighbors in the graph.

2.5 🔴论文中提到的解决方案之关键是什么？

Standard Transformer considers the input tokens as a fully-connected graph, which is agnostic to the intrinsic graph structure among the data.

Motivation: How to be aware of topological structures?

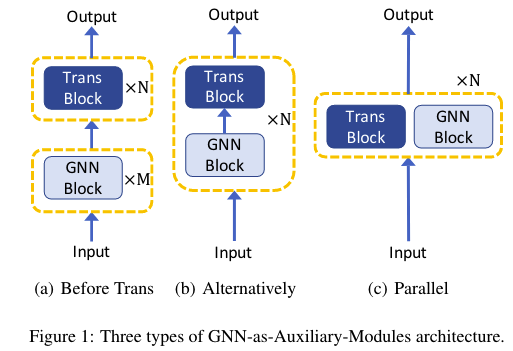
2.5.1 GNNs as Auxiliary Modules in Transformer

According to the relative position between GNN layers and Transformer layers:
1. Building Transformer blocks on top of GNN blocks .
  1. 1. Using Transformer to empower the model global reasoning capability.
  2. Grover
    1. Using two GTransformer modules to represent node-level features and edge-level features respectively.
    2. Inputs are fed into a tailored GNN of each GTransformer to extract vectors as Q, K, V, followed by standard multi-head attention blocks.
  3. GraphiT
    1. Adopting one Graph Convolutional Kernel Network (GCKN) to produce a structure-aware representation from original features
    2. Concatenate them as the input of Transformer architecture.
2. Alternately stacking GNN blocks and Transformer blocks.
  1. Mesh Graphormer
    1. Stacking a Graph Residual Block (GRB) on a multi-head self-attention layer as a Transformer block to model both local and global interactions
3. Parallelizing GNN blocks and Transformer blocks.
  1. Graph-BERT
    1. Utilizing a graph residual term in each attention layer

2.5.2 Improved Positional Embeddings from Graphs

Combining GNNs and Transformer requires heavy hype-parameter searching.

Compress the graph structure into positional embedding (PE) vectors and add them to the input before it is fed to the actual Transformer model:

Compress the adjacent matrix into dense positional embeddings
1. Laplacian eigenvectors（use eigenvectors of the smallest non-trivial eigenvalues as PE）:
2. SVD vectors (use the largest singular values and corresponding left and right singular vectors):
Heuristic methods
1. Degree centrality:
2. WL-PE: Representing different codes labeled by the Weisfeiler-Lehman algorithm.
3. Hop based PE
4. Intimacy based PE
5. Learned PE: Utilizing the full Laplacian spectrum to learn the position of each node in a given graph
...

2.5.3 Improved Attention Matrices from Graphs

Compressing graph structure into fixed-sized PE vectors suffers from information loss.

To improve the attention matrix computation based on graph information: 1. Restricting a node only attending to local node neighbors in the graph: - Extension 1. Encoding edge features: 2. Masking the attention matrices of different heads with different graph priors 3. Extending the adjacent matrix to a kernel matrix: 2. Adding soft graph bias to attention scores: 1. Graphormer: Spatial Encoding mechanism 1. Consider a distance function , such as the shortest path distance (SPD). 2. Assign each feasible value of a learnable scale parameter as a graph bias term. 3. Update rule: 1. is the learnable scalar indexed by 2. To handle graph structure with edge features: - - for each ordered node pair , search (one of) the shortest path from to - is the feature of the -th edge in - is the -th learnable weight embedding 2. Gophormer: proximity enhanced multi-head attention (PE-MHA) to encode multihop graph information. 1. For each node pair , views of structural information is encoded as a proximity encoding vector 2. Update rule: - is the learnable parameters that compute the bias of structural information - The proximity encoding is calculated by M structural encoding functions

2.6 下一步呢？有什么工作可以继续深入？

New paradigm of incorporating the graph and the Transformer.
Extending to other kinds of graphs.
Extending to large-scale graphs