1 📑Metadata
摘要
We propose a recipe on how to build a general, powerful, scalable (GPS) graph Transformer with linear complexity and state-of-the-art results on a diverse set of benchmarks. Graph Transformers (GTs) have gained popularity in the field of graph representation learning with a variety of recent publications but they lack a common foundation about what constitutes a good positional or structural encoding, and what differentiates them. In this paper, we summarize the different types of encodings with a clearer definition and categorize them as being local, global or relative. The prior GTs are constrained to small graphs with a few hundred nodes, here we propose the first architecture with a complexity linear in the number of nodes and edges
by decoupling the local real-edge aggregation from the fully-connected Transformer. We argue that this decoupling does not negatively affect the expressivity, with our architecture being a universal function approximator on graphs. Our GPS recipe consists of choosing 3 main ingredients: (i) positional/structural encoding, (ii) local message-passing mechanism, and (iii) global attention mechanism. We provide a modular framework GRAPHGPS1 that supports multiple types of encodings and that provides efficiency and scalability both in small and large graphs. We test our architecture on 16 benchmarks and show highly competitive results in all of them, show-casing the empirical benefits gained by the modularity and the combination of different strategies.
2 💡Note
2.1 论文试图解决什么问题?
Graph Transformers (GTs) lack a common foundation about what constitutes a good positional or structural encoding, and what differentiates them.
2.2 这是否是一个新的问题?
The principled framework for designing GTs has not been explored before.
2.3 这篇文章要验证一个什么科学假设?
The Transformer, flexible message-passing, and rich positional and structural encodings can all contribute to the success of GPS on a wide variety of benchmarks.
2.4 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?
2.4.1 Graph Transformers (GT)
- Expected to help alleviate the problems of over-smoothing and over-squashing in MPNNs.
- Fully-connected Graph Transformer
- Use eigenvectors of the graph Laplacian as the node positional encoding (PE).
- SAN
- Implement an invariant aggregation of Laplacian's eigenvectors for the PE.
- Use conditional attention for real and virtual edges of a graph.
- Graphormer
- Use pair-wise graph distances (or 3D distances) to define relative positional encodings.
- GraphiT
- Use relative PE derived from diffusion kernels to modulate the attention between nodes.
- GraphTrans: Hybrid architecture
- First use a stack of MPNN layers, before fully-connecting the graph.
- SAT, EGT, GRPE
2.4.2 Positional and Structural Encodings
- Previous works
- Laplacian PE
- Shortest-path-distance
- Node degree centrality
- Kernel distance
- Random-walk SE
- Structural-aware
- Categorization

- PE/SE are:
- used as [[soft bias]], meaning they are simply provided as input features.
- used to direct the messages or create bridges between distant nodes.
2.4.3 Linear Transformers
- Quadratic complexity of attention in the original Transformer architecture.
- Language modeling:
- Linformer
- Reformer
- Longformer
- Performer
- BigBird
- Graph domain:
- Performer-style attention kernelization
2.5 🔴论文中提到的解决方案之关键是什么?
[!Note] Modular GPS graph Transformer, with examples of PE and SE. Task specific layers for node/graph/edge-level predictions, such as pooling or output MLP, are omitted for simplicity.
1. Categorization of PE and SE; 2. How PE and SE increase expressivity; 3. Hybrid MPNN+Transformer architecture.
2.5.1 Modular Positional and Structural Encodings
PE and SE are different yet complementary. 1. PE gives a notion of distance. 2. SE gives a notion of structural similarity. 3. Global --> a text 4. Local --> a sentence 5. Relative --> distance between two words 6. Node --> a word
2.5.1.1 What is PE and SE?
- Positional Encodings (PE)
- Providing an idea of the position in space of a given node within the graph.
- Two close nodes within a graph or subgraph have close PE.
- Previous approach: Computing pair-wise distance between each pairs of nodes or their eigenvectors.
- Linear complexity
PE should either be features of nodes or real edges of the graph. - The eigenvectors of the graph Laplacian.
- Or their gradient.
- Structural Encodings (SE)
- Providing an embedding of the structure of graphs or subgraphs to help increase the expressivity and the generalizability of GNNs.
- Two nodes sharing similar subgraphs or two similar graphs have close SE.
- Previous approach:
- Identifying pre-defined patterns in the graphs as one-hot encodings
Requiring expert knowledge of graphs. - Using diagonal of the m-steps random-walk matrix.
- Using the eigenvalues of the Laplacian.
- Identifying pre-defined patterns in the graphs as one-hot encodings
2.5.1.2 Local
Used as node features.
- Local PE:
- Allow a node to know its position and role within a local cluster of nodes.
- Within a cluster, the closer two nodes are to each other, the closer their local PE will be.
- Local SE:
- Allow a node to understand what sub-structures it is a part of.
- The more similar the m-hop subgraphs around two nodes are, the closer their local SE will be.
2.5.1.3 Global
Used as node or graph features.
- Global PE:
- Allow a node to know its global position within a graph.
- Within a graph, the closer two nodes are, the closer their global PE will be.
- Global SE:
- Provide the network with information about the global structure of the graph.
- The more similar two graphs are, the closer their global SE will be.
2.5.1.4 Relative
Used as edge features.
- Relative PE
- Allow two nodes to understand their distances or directional relationships.
- Edge embedding that is correlated to the distance given by any global or local PE.
- Relative SE
- Allow two nodes to understand how much their structure differ.
- Edge embedding that is correlated to the difference between any local SE.
2.5.2 Why Do We Need PE and SE in MPNN?
- Equivalence between 1-WL test and MPNNs --> limitations of expressive power.
- Using PE and SE as soft biases.
2.5.2.1 1-Weisfeiler-Leman test (1-WL)
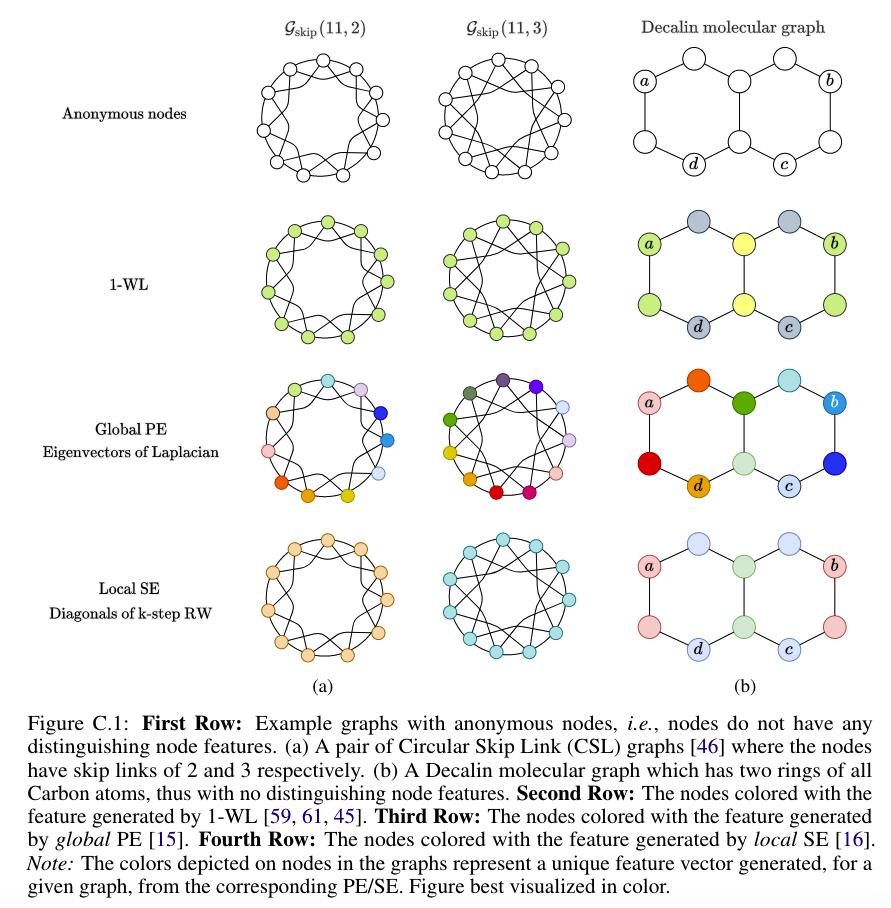
[!Note] About 1-Weisfeiler-Leman test (1-WL) 1. Iteratively updating the color of a node based on its 1-hop local neighborhood 2. Until an iteration when the node colors do not change change successively. 3. The final histogram of the node colors determine whether the algorithm outputs the two graphs to be ‘non-isomorphic’.
[!Note] About Expressive power of MPNNs. 1. The aggregation and update function in MPNNs are at most powerful as the hash function of the [[1-WL test]]. 2. GIN: Graph Isomorphism Network.
- Standard MPNNs are as expressive as the [[1-WL test]],failing to distinguish non-isomorphic graphs under a 1-hop aggregation
- Local, global and relative PE/SE allow MPNNs to become more expressive than the 1-WL test.
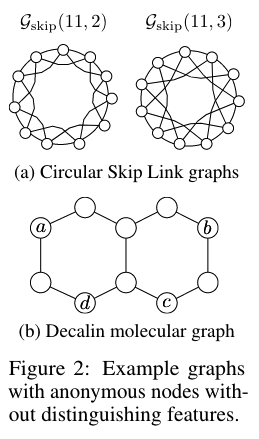
2.5.2.2 Circular Skip Link (CSL) graph
- 1-WL cannot distinguish the two non-isomorphic graphs. -->
Neither does MPNN.
- Using a global PE assigns each node a unique initial color and makes the CSL graph-pair distinguishable.
- Using a local SE can successfully capture the difference in the skip links of the two graphs, resulting in their different node coloring.
2.5.2.3 The Decalin Molecular Graph
1-WL: The combination of the node colors of the node-sets will produce the same embedding for the two links.
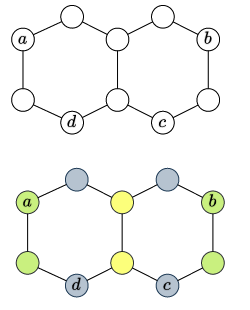
Using local PE is noneffective.
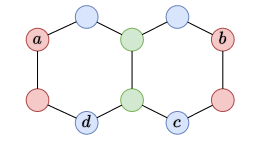
Using a distance-based relative PE on the edges or an eigenvector-based global PE would successfully differentiate the embeddings of the two links.
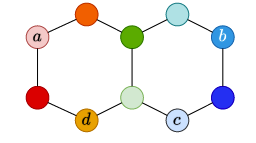
Proposition: there exists Positional Encodings (PE) and Structural Encoding (SE) which MPNNs are not guaranteed to learn.
2.5.3 GPS Layer: an MPNN+Transformer Hybrid
2.5.3.1 Preventing early smoothing
- GraphTrans-style:
- Using a few layers of MPNNs before the Transformer.
- Limitation:
- Due to [[over-smoothing]], [[over-squashing]], and low expressivity against the WL-test, MPNNs irreparably fail to keep some information in the early stage.
2.5.3.2 Update function
[!Note] GPS layers
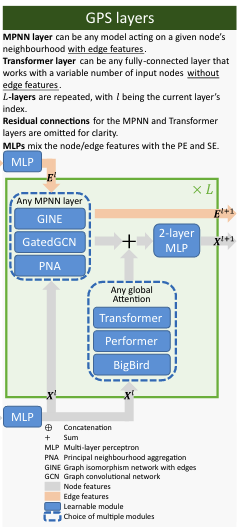
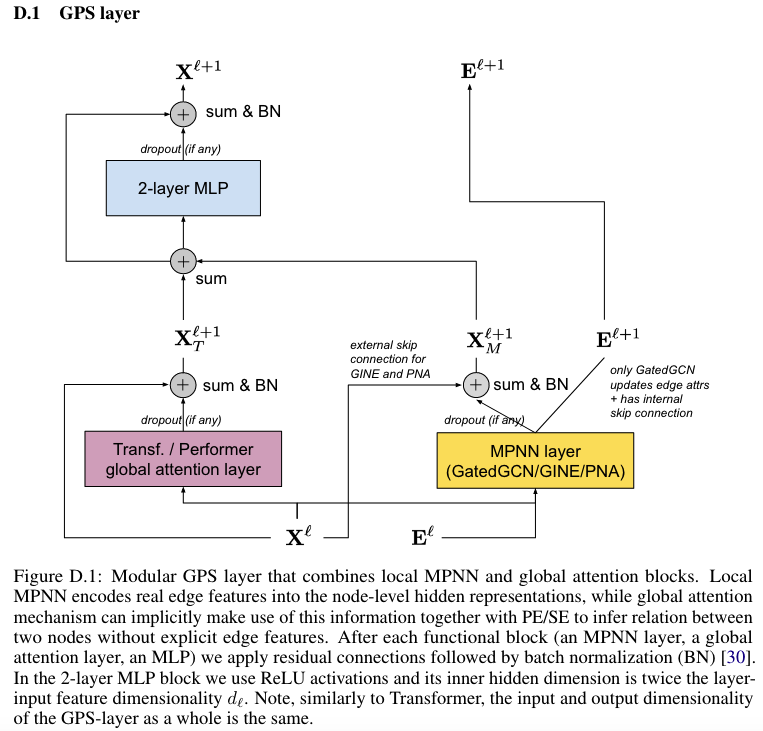
At each layer, the features are updated by aggregating the output of
an MPNN layer with that of a global attention layer.
The precise application of skip connections, dropout, and batch
normalization with learnable affine parameters:
2.5.3.3 Modularity, Scalability and Expressivity
- Modularity
- PE/SE types.
- The networks that processes those PE/SE.
- The MPNN layers.
- The global attention layers.
- The final task-specific prediction head.
- Other layers.
- Scalability
- The computational complexity is linear:
. - A linear Transformer with
complexity. - The complexity of an MPNN is
- A linear Transformer with
- The computational complexity is linear:
- Expressivity
- Does not lose edge information.
- A universal function approximator on graphs.
2.5.4 Theoretical Expressivity
2.5.4.1 Preserving edge information in the Transformer layer
- Previous GTs:
- Graph Transformer, SAN and Graphormer: only use edge features to condition the attention between node pairs.
- GraphiT: does not consider edge features at all.
- 2-step methods (GraphTrans and SAT): use edge features in the first MPNN step --> [[over-smoothing]]
- GPS:
- One round of local neighborhood aggregation via an MPNN layer.
- Global self-attention mechanism.
- Explicitly depends on node features.
- Implicitly encodes edge information.
- Reduces the initial representation bottleneck.
- Enables iterative local and global interactions.
2.5.4.2 Universal function approximator on graphs
- Given the full set of Laplacian eigenvectors, GTs was a universal function approximator on graphs and could provide an approximate solution to the isomorphism problem.
- More powerful than any WL isomorphism test given enough parameters.
2.6 论文中的实验是如何设计的?
Ablation studies + Benchmarking
2.7 用于定量评估的数据集是什么?Baseline 是什么?
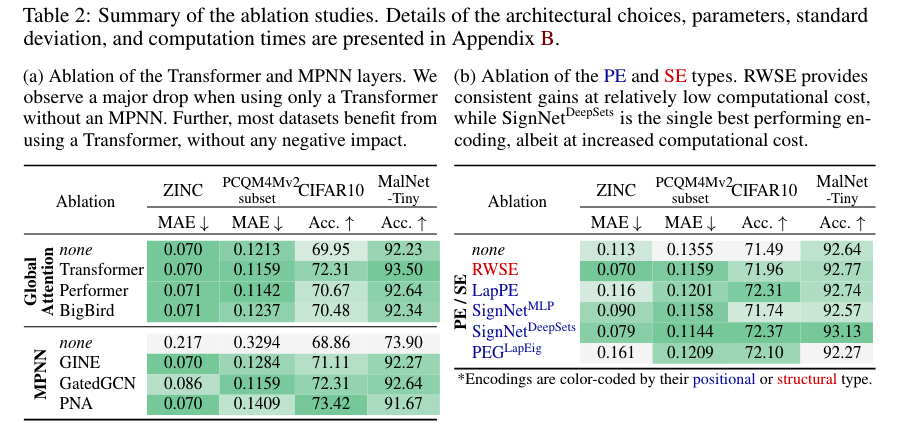
2.7.1 Ablation studies
- Global-Attention module
key-query-value Transformer attention - Linear-time attention of Performer or BigBird
- Message-passing module
- Positional/Structural Encodings
2.7.2 Benchmarking GPS
- 数据集:
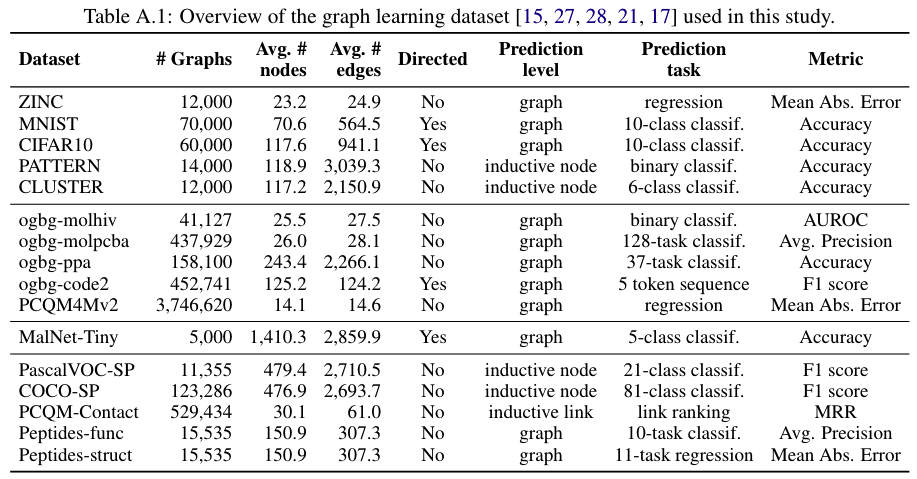
- Benchmarking GNNs: ZINC, PATTERN, CLUSTER, MNIST, CIFAR10
- Graph-level datasets: ogbg-mohiv, ogbg-molpcba, ogbg-code2, ogbg-ppa
- Large-scale challenge: OGB-LSC PCQM4Mv2
- Long-Range Benchmark: MalNet-Tiny
- 基线:
- Popular message-passing neural networks (GCN, GIN, GatedGCN, PNA, etc.)
- Graph transformers (SAN, Graphormer, etc.)
- Recent graph neural networks with SOTA results (CIN, CRaWL, GIN-AK+, ExpC)
2.8 论文中的实验及结果有没有很好地支持需要验证的科学假设?
2.8.1 Ablation studies
实验结果:
结论: 1. Global-Attention module: 1. Transformer is always beneficial. --> Long-range dependencies are generally important. 2. Message-passing module: 1. Fundamental to the success of GPS. 3. Positional/Structural Encodings: 1. Generally beneficial to downstream tasks. 2. The benefits of the different encodings are very dataset dependent.
2.8.2 Benchmarking GPS
实验结果: 1. Benchmarking GNNs
2. Graph-level OGB benchmarks
3. PCQM4Mv2
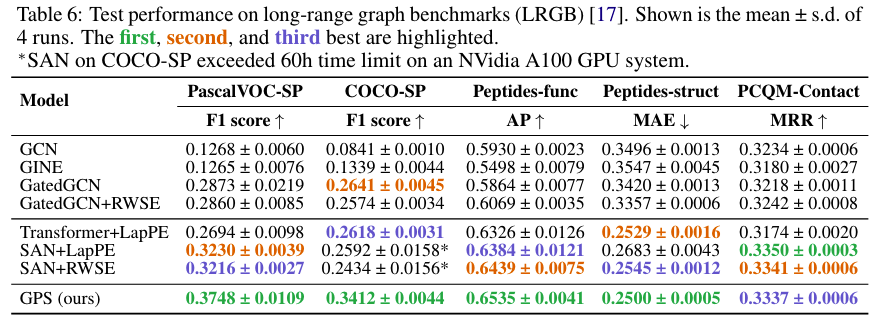
4. Long-range graph benchmarks (LRGB)
结论: 1. Benchmarking GNNs --> Expressiveness 2. Open Graph Benchmark --> Versatility 3. OGB-LSC PCQM4Mv2 --> Comparable parameter budget 4. MalNet-Tiny --> Scalability 5. Long-Range Graph Benchmark --> Ability to capture long-range dependencies
2.9 这篇论文到底有什么贡献?
- Provide a GT blueprint that incorporates positional and structural encodings with local [[message passing]] and global attention.
- Provide a better definition of PEs and SEs and organize them into local, global, and relative categories.
- Apply GTs with linear global attention to larger datasets.
2.10 下一步呢?有什么工作可以继续深入?
- GTs are sensitive to hyper-parameters and there is no one-size-fits-all solution for all datasets.
- A lack of challenging graph datasets necessitating long-range dependencies.