1 📑摘要与结论
1.1 摘要
原文: In several applications the information is naturally represented by graphs. Traditional approaches cope with graphical data structures using a preprocessing phase which transforms the graphs into a set of flat vectors. However, in this way, important topological information may be lost and the achieved results may heavily depend on the preprocessing stage. This paper presents a new neural model, called graph neural network (GNN), capable of directly processing graphs. GNNs extends recursive neural networks and can be applied on most of the practically useful kinds of graphs, including directed, undirected, labelled and cyclic graphs. A learning algorithm for GNNs is proposed and some experiments are discussed which assess the properties of the model.
翻译:在一些应用中,信息自然用图形表示。传统方法使用预处理阶段处理图数据结构,该阶段将图形转换为一组平面向量。然而,这样做可能会丢失重要的拓扑信息,所获得的结果可能在很大程度上取决于预处理阶段。 本文提出了一种新的神经模型,称为图神经网络(GNN),能够直接处理图。GNN扩展了递归神经网络,可以应用于大多数实际有用的图类型,包括有向图、无向图、标记图和循环图。本文提出了一种GNN的学习算法,并讨论了一些评估模型性能的实验。
1.2 结论
原文:A new neural model, called graph neural network (GNN), was presented. GNNs extend recursiveneural networks, since theycan process alar ger class of graphs and can be used on node focused problems. Some preliminary experimental results confirmed that the model is very promising. The experimentation of the approach on larger applications is a matter of future research. From a theoretical point of view,it is interesting to study also the case when the input graph is not predefined but it changes during the learning procedure.
翻译:提出了一种新的神经网络模型,称为图神经网络(GNN)。GNN扩展了递归神经网络,因为它们可以处理一类更大的图,并且可以用于以节点为中心的问题。一些初步实验结果证实了该模型是非常有前景的。该方法在更大规模应用上的实验是未来研究的问题。从理论的角度来看,研究输入图形不是预定义的,而是在学习过程中发生变化的情况也是很有趣的。
2 💡笔记
2.1 论文试图解决什么问题?
在一些应用中信息用图形表示。传统方法将图形转换为一组平面向量来处理图数据结构,这样做可能会丢失重要的拓扑信息,所获得的结果也可能在很大程度上取决于预处理阶段。
2.2 这是否是一个新的问题?
图数据处理在本文以前已有很多研究工作。
2.3 这篇文章要验证一个什么科学假设?
论文要验证的是:本文提出的图神经网络模型(GNN)可以很好地直接处理图数据。
2.4 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?
- 应用:
- Node focused --> Object Localization
- Graph focused --> Image Classification
- 传统的应用通常通过预处理过程来处理图形,该预处理过程将图形转换为更简单的表示形式(例如,向量或实数序列)
- 性能和泛化性都很差
- RNN来直接处理图数据:将图信息编码为与节点相关联的一组状态,状态根据节点之间的拓扑关系动态更新,最后使用存储在状态中的编码计算输出
- RNN只能处理有向图和无环图
- 只能用于以图为中心的问题
2.5 🔴论文中提到的解决方案之关键是什么?
2.5.1 主体框架
符号说明
- 图
是 对,其中 是节点集, 是边集。 - 用圆弧连接到
的节点用 表示。 - 每个节点n都有一个标签
- 图中的节点n表示对象或概念,而边e表示它们的关系。
为节点状态 为n的邻居节点的标签
- 图
为每一个节点n附加一个状态向量
,包含邻居节点的信息,构建==transition function==: 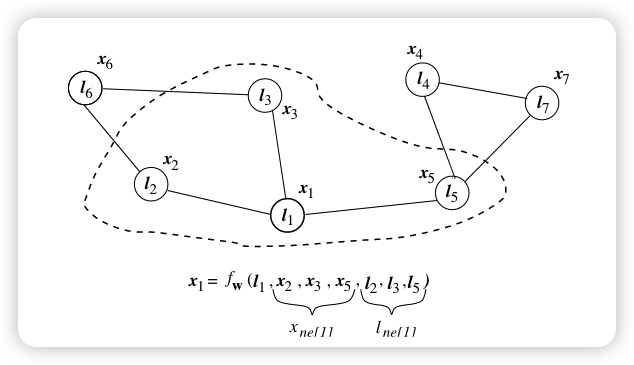
构建==output function==计算输出:
计算所有的状态和标签,得global transition function 和 global output function:
Loss函数:
,其中
2.5.2 需要关注的问题
如何求解
:Banach不动点原理 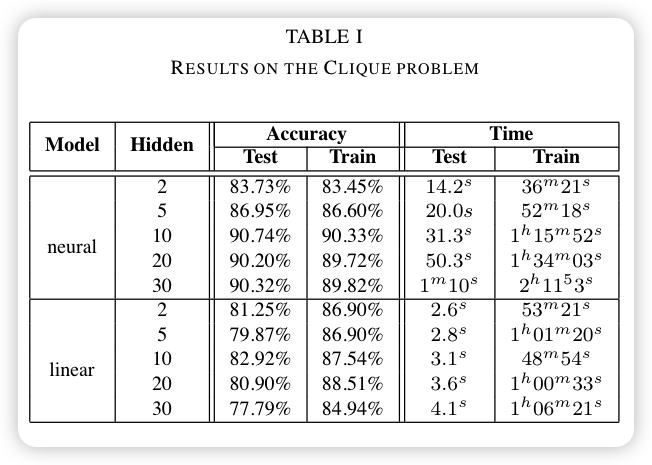
如何学习两函数中的参数
Step 1: 状态
Step 2: 计算损失梯度
- 如何实现这两个函数
- Linear GNN:
其中:
2.6 论文中的实验是如何设计的?
- 使用3层带sigmoid激活函数的FNN来实现两个模型中的函数
- 状态的维度为2
- 实验结果取5次平均值
- train 5000 epochs 每20 epochs验证一次
2.7 用于定量评估的数据集是什么?评估标准是什么?Baseline是什么?
2.7.1 Connection-based problems
- The Clique problem:
- 数据集: 1400个带有20个节点的随机图:train 200 + val 200 + test 1000
- 输入: 1个图
- 输出: 是否有size为5的clique(True = 1, False = -1)
- 指标: Accuracy, Time
- 基线:
- neural (Hidden = [2, 5, 10, 20, 30])
- linear (Hidden = [2, 5, 10, 20, 30])
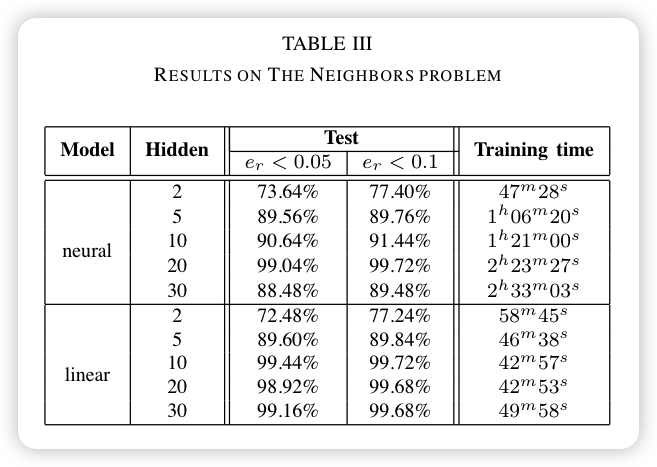
- The Neighbors problem:
- 数据集: 一个有500个节点的图:train 100 + val 100 + test 300
- 输入: 1个node
- 输出: 该node的所有邻居节点的个数
- 指标: absolute relative error,Training time
- 基线:
- neural (Hidden = [2, 5, 10, 20, 30])
- linear (Hidden = [2, 5, 10, 20, 30])
- The 2-order Neighborsproblem:
- 数据集: 一个有500个节点的图:train 100 + val 100 + test 300
- 输入: 1个node
- 输出: 该node的所有邻居节点的个数 + 所有邻居的邻居节点的个数
- 指标: absolute relative error,Training time
- 基线:
- neural (Hidden = [2, 5, 10, 20, 30])
- linear (Hidden = [2, 5, 10, 20, 30])
2.7.2 Label-based problems
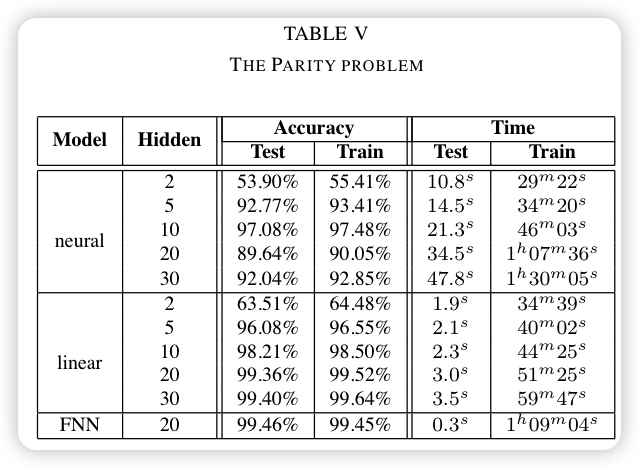
- The Parity problem:
- 数据集: 2500个图:(train + val) 500 + test 2000,每张图上的每个节点有一个包含8位布尔元素的向量(定义如果该向量有偶数个1则为偶节点,反之为奇节点)
- 输入: 1个节点
- 输出: 该节点是否为偶节点(True = 1, False = -1)
- 指标: Accuracy, Time
- 基线:
- neural (Hidden = [2, 5, 10, 20, 30])
- linear (Hidden = [2, 5, 10, 20, 30])
- FNN (Layers = 3, Hidden = 20)
2.7.3 General problems
- The Subgraph Matching problem:
- 数据集: 600个相连的随机图:train 200 + val 200 + test 200
- 输入: 1个节点
- 输出: 该节点是否属于随机生成的子图(True = 1, False = -1)
- 指标: Accuracy
- 基线(子图节点个数 = [3, 5, 7, 9];图节点个数 = [6, 10, 14, 18]):
- neural GNN(State_dim = 5, Hidden = 5)
- neural linear FNN(Hidden = 20)
2.8 论文中的实验及结果有没有很好地支持需要验证的科学假设?
2.8.1 Connection-based problems
- The Clique problem
结论: 1. GNN模型在该实验中没有遇到泛化性问题; 2. 隐藏神经元的个数对Nerual GNN结果有显著影响,对Linear GNN的结果影响不明显; 3. 每个Epoch的时间长短与数据集和网络大小都有关
- The Neighborsproblem & The 2-order Neighborsproblem
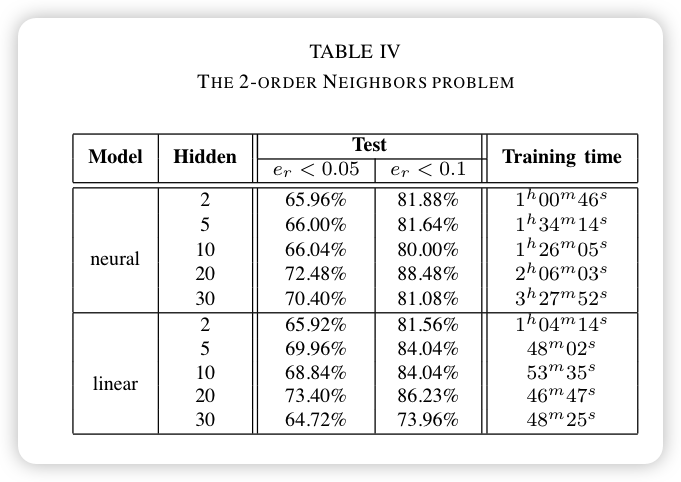
2.8.2 Label-based problems
The Parity problem: 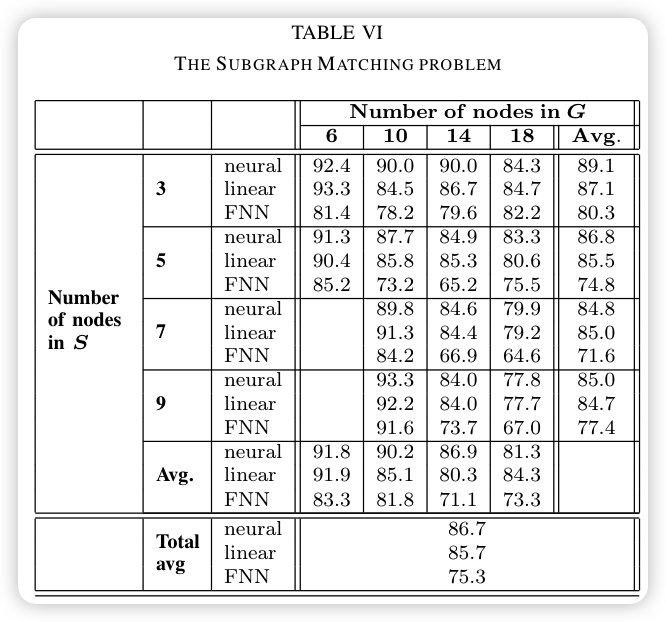
结论:GNN模型能够在解决问题不需要此类信息的情况下丢弃图拓扑中包含的信息。
2.8.3 General problems
The Subgraph Matching problem: [[A new model for learning in graph domains_image_7.png]]
2.9 这篇论文到底有什么贡献?
提出了GNN模型来处理很多图问题,实验表明该模型很有前景。
2.10 下一步呢?有什么工作可以继续深入?
如何解决图未先定义条件下的GNN学习问题。
